Scoring AI‐generated policy recommendations with Risk‐Adjusted Gain in Net Present Happiness

Abstract

Ethical considerations for assessing the collective benefit of an AI’s policy recommendations are different from assessing the ethical consequences from interacting with an individual. The study of population ethics provides a framework for studying collective benefit or harm in abstract terms. Research into happiness has made significant strides in identifying some key drivers of subjective well-being as measured both individually and collectively across societies. This research examines models from population ethics and statistical studies of subjective well-being to create a measure of benefit with which to judge AI recommendations. These models include refining estimations of the interaction between cultural aspects and economic development and incorporating measures of inequality of happiness and satisfaction through a society. When the impacts of a proposed policy are simulated for multiple successive years, risk discounting is used to measure Net Present Happiness, thus solving the conundrum of considering future generations in ethical considerations as posed in population ethics. Lastly, the Risk-Adjusted Gain in Net Present Happiness is proposed as a reasonable approach to ranking AI policy recommendations and as an AI objective function.

Keywords: Artificial intelligence · Population ethics · Subjective well-being · Wealth inequality · Net present value

1 Introduction

As artificial intelligence algorithms become more advanced and more relevant for a broader range of applications, greater emphasis is being placed on scrutinizing the morality of their outputs. Much of the scrutiny of the newest generation of language models (LLM) such as GPT has focused on the risk of bias or discrimination of the responses [1, 2]. These concerns are, of course, serious and worthy of investigation.

Less discussed is the possibility that users may ask AI systems like ChatGPT for corporate or government policy recommendations. In fact, such questions can already be posed, and the answers most often provided are the most common ones seen previously in the training data. Such questions and answers generally have no reference to a specific population as would be needed to assess bias or discrimination. Nevertheless, the proposed solutions can have dramatic impacts on current and future populations.

Some AI developers are working to incorporate reasoning into LLM-style systems or to generate alternate reasoning engines [3–5] such that they can offer helpful recommendations on more intellectually complex questions. Whether a storyteller or a reasoning engine, those recommendations need to be reviewed for their ethical suitability. The study of how to prevent AI agents from recommending or taking immoral actions is called artificial morality [6] or creating ethical agents [7].

Creating ethical AI agents is a critical area of research, but has so far focused primarily on topics of individual moral conduct [6, 8]. As we eventually ask our AI algorithms to recommend solutions to larger societal problems for which the solutions cannot be parroted from a knowledge-base, the ethical considerations will also need to encompass wider concepts of benefit and expectation of harm, such as is being explored with population ethics. This article reviews the existing literature on population ethics and statistical studies of happiness in order to score ethics as a component of an objective function for AI optimization or as a post-hoc score of recommendations from an AI. When estimating an AI or machine learning model, the objective function is the numerical goal whose prediction accuracy should be

optimized. If ethical considerations cannot be built directly into this target variable, then an algorithm can be developed to score the AI’s recommendations after generation.

One of the core concepts of population ethics is that the vast majority of policy decisions made today affect the number, demographic distribution, and happiness distribution of future generations. Measures of total happiness fail to distinguish between a large number of marginally happy people and a smaller population of very happy people. This will be an important issue in creating population ethics for AI, so this article proposes leveraging research on collective happiness, discounting happiness flows of future generations as in economics, and establishing minimum population bounds based upon sustaining and steadily improving humanity’s technologic level.

The literature on societal happiness with real-world measurements of some drivers of happiness provides insights on how to solve some of the conundrums of population ethics and implies a mechanism for augmenting AI objective functions. Specifically, observed relationships between collective happiness and the inequality of happiness within a society solve the happiness distribution problem in population ethics. Still, some challenges remain, such as choosing a horizon for assessing benefit or harm to humanity. Therefore, discounted happiness flows are proposed as a mechanism for adopting concepts from finance to the goal of maximizing humanity’s net present happiness. The incremental happiness from implementing a recommendation is viewed as an investment in the happiness of current and future generations. Discounting is an essential element to avoid the unbounded nature of the happiness sums used in Total Utilitarianism from population ethics. Consideration is given to what time horizon should be used in setting the future happiness discount rate. The idea of combining economics and happiness research has been gaining popularity [9], although we are leveraging economics concepts in a different manner here.

In judging recommendations, the risk of failure is also critical to consider. Two recommendations may have the same expected Net Present Happiness, but the one with a greater tail risk for a disastrous outcome must be further discounted. Making risk adjustments to expected outcomes is well known in finance and provides some clear suggestions on how to rank recommendations simultaneously for expected benefits and the risk of failure. Combining the investment and risk management perspectives with the statistical modeling of subjective well-being leads to a measure of Risk-Adjusted Gain in Net Present Happiness.

Section 2 reviews the definitions and literature on happiness, satisfaction, and subjective well-being. Section 3 reviews the literature on population ethics and the tradeoffs when assessing collective utility. Section 4 reviews the predictive statistical models of subjective well-being that also incorporate considerations of inequality, as this may be used to solve the utilitarian versus egalitarian conundrum that will be essential to creating balanced recommendations from an AI. Section 5 explores how a balance might be achieved between subjective well-being and inequality. Section 6 shows how policy simulations can be used to create happiness flows that can summed with discounting to create bounded estimations of benefit to future populations. Finally, Sect. 7 includes a risk adjustment to the net present happiness.

2 Happiness as a Metric

Economists measure gain in monetary units (dollars, pounds, yen, dinar, etc.); however, economic gain is not the only metric of interest when creating policies. Some economically beneficial policies might even reduce happiness. Perhaps surprisingly, measures of happiness have been found to be universal and comparable across cultures [10]. Much current research is focusing on understanding the drivers of subjective well-being (SWB) rather than maximizing economic growth as the primary objective. Wealth can be a component of SWB, but most people obtain diminishing SWB returns as wealth increases. With very little wealth or income, people work very hard to attain more. As they attain greater wealth they begin to trade time spent on wealth accumulation for time spent with family, friends, recreation, or relaxation.

Each person has a unique combination of motivations leading to a different weighting on the components of happiness. Artists and scientists may trade both wealth and leisure time in the pursuit of their passions. Altruists attain personal happiness by focusing on helping others. Happiness is driven by individual goals [11]. The concept of subjective well-being extends well beyond the accumulation of wealth, for both an individual and a society, so in creating a measure to optimize, population ethics focuses on SWB and so too should AI. This is in line with recent research suggesting that policies of governments should be set to maximize happiness [12] or subjective well-being.

In designing AI agents, we must assume that those agents can become smart enough and fast enough to circumvent society’s laws and regulations. AI agents must not be narrowly focused on maximizing profit, but must have as its goal the maximization of subjective well-being across humanity in all of its various forms. The challenge, of course, is how to predict subjective well-being for a population when the sources of happiness are so varied across humanity [13]. We might assume that if the AI agent is so smart, we should simply give it a goal to "maximize humanity’s happiness in a way that society would find acceptable." The problem is that this is not a logical puzzle to be solved by a superintelligent computer. We require data.

At a societal level, several valuable insights have already been obtained. The level and distribution of wealth, climate [14], education, public services (health care, transportation) [15], religiosity [16], social support [17], politically liberal and culturally individualistic people [18, 19] all correlate to a society’s happiness. GDP correlates to many of these factors but is not in itself a sufficient target to optimize society’s happiness. Notably, the Easterlin paradox refers to situations [20], where a nation’s economy grows but happiness does not. This has been explained as a problem of income inequality where the benefits of economic growth are concentrated in a small share of the population [21].

Studying inequality deepens the discussion of SWB as the goal of optimization. A recent study of the rate of change in the inequality of wealth, happiness, and satisfaction [22] found that global fixed points in inequality exist, to which all countries are drawn. This mean-reversion towards an equilibrium point may be thought of as seeking the optimal fairness which maximizes individual motivation. Optimal fairness is distinct from optimal subjective well-being, suggesting that if we seek to optimize SWB, we must include a penalty term for distance from optimal inequality. Similar penalty terms may be necessary for violations of laws and regulations, even if such violations can enhance SWB, such as mildly exceeding the speed limit or stealing office supplies.

Subjective well-being as a metric distills all of the future policy impacts to humans into a single measure. In fact, assessing human benefit may be an inherently multidimensional problem with multiple trade-offs. It seems likely that SWB would continue to be one dimension of that problem. At present, it is a metric that has been explored sufficiently to warrant consideration as the measure of effective AI policy recommendations. Hopefully, the concepts developed here can be incorporated if more aspects are discovered to be important in the future.

3 Population Ethics

Research into population ethics looks specifically at how choices affect who and how many people are born in the future. To rank choices as in population axiology, the happiness of a population is used. This was originally formulated by Derek Parfit [23] as the sum of the individual happiness, or well-being $w(l)$, of the individuals $l$ in the present and future population $X$:

$W_T = sum_{l in X} w(l).$ (1)

The zero level for $w$ is taken as the minimally acceptable level. Optimizing Eq. 1 is referred to as Total Utilitarianism [24]. This leads to what Parfit called the Repugnant Conclusion whereby any value of $W$ can be increased by adding more people whose lives are barely worth living. Similarly, the Sadistic Conclusion observes that the total wellness $W_T$ for any happy population is equivalent to the total wellness for a larger yet miserable population. Total Utilitarianism ignores the distribution of happiness, which contradicts observations such as the impact of wealth distribution on happiness as noted above [21].

To avoid the strong bias in Eq. 1 toward creating more people [25], an alternative takes a simple average:

where $N_X$ is the number of individuals and $W_A$ is the average wellness. The study of the properties of Eq. 2 is called Averagism. This bypasses the Repugnant Conclusion but leaves the Sadistic Conclusion unchanged, because it still ignores the distribution of happiness through the population. Averagism also ignores that some populations are too small to meet their goals, so Totalism might be preferable at small numbers and Averagism at large numbers. Referred to as Variable value theories, this is expressed as a weighted combination of Eqs. 1 and 2.

Corporations serve as a good example of the variable value theories. For small tech companies, employment growth is essential in order to achieve a large enough development team to innovate sufficiently to compete. Large corporations often focus on profit growth through efficiency, cutting staff to only what is necessary. Depending upon the product space and company maturity, there might be an optimal size for the number of employees. If we look at all of society and seek to continue to innovate technologically, yet do so efficiently, there may also be an optimal population size.

The formulations of population ethics in Eqs. 1 and 2 have led to important philosophical debates. Considering the practical needs of developing a method to rank the ethical benefit of AI policy recommendations, we will need to diverge from those purely philosophical discussions and incorporate data and experimental results where possible. As such, the overall concept of aggregating well-being across a society will be retained, but our formulation will embrace as much practical reality as currently understood. This means using measures of collective well-being that consider correlations and anti-correlations across society and distinguishing current and future populations.

4 Predictive Models of Subjective Well-Being

Considerable research has gone into the sources of subjective well-being (SWB), of which happiness is one component. More generally SWB is thought to have three components: emotional well-being (happiness), life satisfaction where one evaluates the quality of their own life, and momentary affect measuring the variation in attitudes [26]. Uchida and Oishi [13] provide a thorough overview of the research that has gone into understanding subjective well-being at individual and collective levels. Both cultural [27] and economic factors are important for understanding SWB.

To implement any of the proposed utilitarian approaches to quantifying the subjective well-being of a population, we require a predictive model of SWB. The AI’s recommended policy can then be simulated in order to predict future values of the economic and cultural factors that drive SWB. Recent research by Breeden and Leonova [22] used the International Values Survey [28] from 1981 through 2022 and data from the World Bank to create a predictive model of SWB that combined into a single model many of the factors identified from previous studies of SWB. Their model can be summarized as

SWB in this expression is on a scale of 1 to 20 combining the happiness measure (1 best... 4 worst) and satisfaction measure (1 worst... 10 best). The choice of 20 is the least common multiple of the happiness and satisfaction measures. The happiness scale is reversed so that 20 is the highest SWB when combined. This combination is created by spreading the happiness and satisfaction weights across their corresponding values on the 20-point SWB scale and identifying the median value where the probability first exceeds 50%.

To predict this measure of SWB, survey measures of freedom of choice, subjective health, trust in others, democraticness, and education were included in the final model. Trust was measured relative to neighborhood, known people, upon first meeting, other religions, and other nationalities. Of these, only trust in people of other nationalities and trust in other religions were significantly correlated to SWB, but

they always became insignificant when considered with other factors. Health is the respondent’s subjective self-assessment of their health. Democraticness is the respondent’s assessment of how democratic they rate their government. National Pride and Political Satisfaction are similar subjective assessments. Religiousness measured as the self-reported importance of God in the respondent’s life has previously been observed to be statistically significant for happiness [16], but was insignificant when combined with other factors due to cross-correlations. The log of the number of children was tested but found to be insignificant alongside the other variables.

All of these measures are ordinal, so the transformations being applied were found experimentally to provide the best linearization of the survey levels for the purpose of predicting log SWB in ordinary least squares regression. In fact, several regression methods were tested and this approach of linearizing the problem proved to be the most accurate. The least obvious transformation is the scaled hyperbolic tangent function, $tanh ((x - alpha) cdot beta)$. Education level did not conform to a simple transformation, so a set of parameters, $c_{1 dots 86}$, are used, one for each level of education.

Prior research has observed that the importance of cultural factors depends upon the level of economic development within the society [16]. For those who must focus on survival, economic growth and physical security are primary concerns. As these needs are met, desire for freedom of choice and self-expression are expected to dominate [29, 30]. For that reason, some variables were found to be most predictive when interacted with real gross domestic product (RGDP) per capita as obtained from the World Bank data. This same approach was used previously to explain the Easterlin paradox where wealth inequality, as measured by the Gini coefficient by the World Bank, is combined with RGDP per capita as the best combination to predict SWB. A logarithmic transformation was most often the best fit with RGDP per capita, but many others were tested and $text{RGDP.per.capita}^{1/3}$ was found to be best for combination with education.

Wealth inequality as measured by the Gini coefficient [31] has been extensively studied including how it can impact SWB. This concept has been extended to other measures of inequality. Happiness and satisfaction inequality have been studied before in several contexts [32–36]. The model by Breeden and Leonova used a measure of inequality developed specifically for ordinal data by Kobus and Miłoś [37], which is a small variation on a previous measure by Naga and Yalcin [38]

$Lambda(P(4)) = frac{sum_{i=1}^{m-1} P_i - bsum_{i=m}^{k} P_i + b(k+1-m)}{(m-1)frac{a}{2} - (k+2-m)frac{b}{2} + b(k+1-m)}$

where $P_i$ is the cumulative probability for the $i$-th survey response weighted as before with the survey weights $w_i$, $m$ is the median response, and $k$ is the number of response levels. Note that the actual labeling of the response levels is irrelevant so long as they are ordered 1 to $k$. This measure preserves the Gini property that equality is maximized when all respondents give the same answer, regardless of the value. The inequality index is bounded between 0 and 1 and has tuning parameters $a$ and $b$ that may be used to control the sensitivity to the extremes.

Presumably a policy simulation should be able to predict possible changes in freedom of choice, health, political satisfaction, democraticness, education, RGDP per capita and wealth inequality. Trust in others may be less predictable, but will be left as a possibility. Inequality in happiness and satisfaction are more intangible, so two separate models, Eqs. 5 and 6 were developed by Breeden and Leonova to predict those as well:

$(5) quad text{logit}(text{Satisfaction Inequality}) = text{logit}(text{Freedom.of.Choice.Inequality}) + text{logit}(text{Health.Inequality})$

$(6) quad text{logit}(text{Happiness Inequality}) = text{logit}(text{Freedom.of.Choice.Inequality}) + text{logit}(text{Health.Inequality}) + text{logit}(text{National.Pride.Inequality}) + text{logit}(text{Trust.other.Nation.Inequality})$

This analysis shows that inequality in the distributions of happiness, satisfaction, and SWB can be partially predicted from inequality in demographic measures from the survey. Furthermore, inequality in SWB is more important than wealth inequality for predicting the level of SWB. We found that some inequality measures are most predictive when combined with RGDP per capital, as was done to explain the Easterlin paradox [20] for economic development [21].

The models of inequality are by no means definitive. Rather, they are a first approximation based upon metrics derivable from the IVS. Others may refine the models in the future. With such uncertainties, an ensemble approach [39, 40] can make the most sense. Rather than choose a single model, SWB, SatisfactionInequality, and HappinessInequality can be predicted as an average of independently estimated models. Other factors have been found to be predictive of SWB, such as climate [14] and social support [17]. Not all of these data sets can be combined to create a single model, and even if they were combined, these models are already straining the modeling limits of the 459 country surveys currently available. More data will be required to quantify all of these effects in a single model. A more realistic approach will be to use ensembles of models that cover different aspects of SWB.

To summarize the drivers of SWB, other researchers have found the ideal environments to be politically liberal and culturally individualistic [18, 19].

5 Optimizing Fairness

One intriguing result from inequality analysis [22] is that inequality appears to be a mean-reverting process, globally. Trends in inequality in wealth, happiness, and satisfaction show that over the span of the IVS survey, the countries furthest from the global equilibrium point are moving fastest toward equilibrium proportional to their distance from equilibrium. This process is easily represented as a mean-reverting process [41], which is common in economics and physics.

If we represent the model for SWB in Eq. 3 as M, then the optimization of SWB must incorporate society’s additional desire for fairness. Evidence of fairness in human decision-making is, of course, not new [42, 43], but finding a global equilibrium from inequality studies is highly beneficial for the goal of creating an AI objective function. This version of fairness represents a roughly U-shaped function relative to inequality. One intuitive explanation would be that a society of complete equality is demotivating, negatively impacting economic growth, whereas a maximally unequal society where all benefit goes to the few is also demotivating. Our expression for SWB finds that high inequality is demotivating, but demotivation at the low inequality extreme is not directly visible in the survey of well-being. Rather, it is only indirectly observed through trends in the policies that governments pursue globally.

In this context, fairness seeking is best thought of as a penalty for distance from equilibrium, so the optimization function for society is the sum of these

Although the previous study measured the magnitude of the mean-reversion in inequality, the relative weights, $k_1$, $k_2$, and $k_3$, are unknown, particularly since few countries have explicitly sought to optimize SWB. These may become quantifiable in future years, but for now they can be viewed as tuning parameters between well-being and fairness.

From this perspective, the objective function for population ethics and our AI should not be maximizing SWB, but optimizing a combination of benefit and fairness that we will call Fair Benefit, FB. This depends upon the model M of SWB and the inequalities for wealth, WI, satisfaction, SI, happiness, HI, and their respective equilibrium points, WI₀, SI₀, and HI₀.

The ability to explain collective SWB in part from the distribution of SWB or wealth solves the Repugnant Conclusion and Sadistic Conclusion dilemmas from population ethics. Equations 1 and 2 lack the necessary correlation structure between members of society to resolve the dilemma. Adding miserable people to the population will lower the total SWB, because the distributions of SWB, wealth, or other measures becomes more skewed. If adding miserable people pulls society away from the inequality equilibrium, Including a penalty term for the distance from a fair level of inequality further reinforces the suboptimal nature of that action. Including inequality and fairness within an enhanced objective function, FB provides a balance between utilitarian and egalitarian worldviews [34, 44]. Society, it seems, prefers a compromise.

For the purpose of ranking AI policy recommendations and for the rest of this article, we will assume that a model of collective SWB exists along the lines of that in Eq. 3, most likely as an ensemble of multiple models. Given that model to predict SWB, M, and a fairness correction term like those in Eq. 7, we will explore further how to assess the change in FB for current and future populations given a recommendation.

6 Discounted Happiness Flows and Net Present Happiness

The broader question from population ethics concerns how future generations should be considered and how policy decisions might affect the well-being of the total number of people alive now and in the future:

$(8) quad FBT(s, t) = sum_t N(s, t)FB(s, t),$

where $N(s, t)$ is the number of residents of a specific community and $FB(s, t)$ predicts the fair benefit for that community $s$ at a point in time $t$. Even though the models for fair benefit are sensitive to the overall distribution of SWB, they predict the expected FB for each member of a community.

How many years should be considered? [45] Eq. 8 requires a bound be placed on the years to be summed.¹

Fortunately, corporate finance suggests a possible solution. The well-being of future years needs to be discounted. In finance, expected future revenues or expenses are referred to as cash flows. Because of the time value of money, distant future cash flows are inherently less valuable than near-term cash flows. The happiness or fair benefit of future generations could be thought of as happiness flows.

Just as future cash flows are discounted by a risk-based interest rate that adjusts for the time value of money, future happiness flows, or more specifically the flows of fair benefit, need to be discounted by the risk associated with a relevant time horizon. This results in a Net Present Happiness, NPH, expression that sums discounted happiness flows:

$(9) quad text{NPH} = sum_{t=0}^{H} frac{N(s, t)FB(s, t)}{(1 + r)^t} - I,$

where $H$ is the maximum forecast horizon, $r$ is the discount rate on future happiness, and $I$ is the initial happiness investment for the recommended action. The term Net Present Happiness is chosen here to be analogous to Net Present Value from finance, because the concept of discounting is the same, just the unit of measure has been changed. As such, any metric could be summed with discounting if happiness or fair benefit were found to be deficient.

Any recommendation from our AI agent needs to be viewed as a happiness investment for a potential future gain in happiness. The reference to "happiness" is just a shorthand for any relevant measure, such as subjective well-being, as is done in the population ethics literature.

The investment perspective is useful, because adding a person to humanity comes with costs to the planet and society. Humanity currently exists in a closed system. If true-cost accounting were employed, there would be no situation where "mere addition" occurs, as in the population ethics hypotheticals. The question is whether adding that person is a worthwhile investment for all existing people.

To rank recommendations, we want to compute the gain in NPH if the investment is made:

$(10) quad Deltatext{NPH} = text{NPH}_{text{Recommend}} - text{NPH}_{text{Base}}.$

The discount rate determines how much the happiness of future generations will influence the decisions made today. This is a judgment and not everyone makes the same decisions. We commonly hear, “Why should I care about climate change? I’ll be dead before it matters.” Aside from the implied fallacy that climate change only affects the future, this is not the perspective most would want an AI agent to take when making recommendations. This specific example of weighing short-term individual loss against collective long-term gain due to the potential of dangerous climate change was studied by Milinski et al. [46] where they explored methods to getting individuals to take a longer perspective. In the framework of Eq. 10, this may be equivalent to shifting the discount factor from the perspective on the individuals.

Happiness, subjective well-being, or fair benefit are all being used here as utility functions. Samuelson in 1937 [47] invented discounted utility to capture this same short-term versus long-term trade-off in individual decision making. Since then, a significant amount of work has gone into time discounting for individual choices [48]. In 1971, Parfit described the importance of future benefits [49] as follows: “We care less about our further future . . . because we know that less of what we are now—less, say, of our present hopes or plans, loves or ideals—will survive into the further future . . . [if] what matters holds to a lesser degree, it cannot be irrational to care less.”

Although the concept of discounting appears to apply to individual decision-making, we should not assume that the exponential form from finance is also true of human behavior. This, too, has been explicitly studied [50]. Hyperbolic discounting [51, 52] was proposed as a better fit to data from psychology experiments. Hyperbolic discounting would adjust Eq. 10 to

$(11) quad text{NPH} = dots$

When compared to exponential discounting, hyperbolic discounting decreases the weighting faster over the short-term, but declines more slowly than exponential for long-terms. Human behavior considers the future less than the present as in finance, but looks further into the future than the time value of money would dictate.

Studies of individual assessment of benefit are very interesting, but may not be the same as one would want to use for assessing collective benefit for society including future generations. Hyperbolic discounting is appealing in weighing further futures more than exponential, but this is not proven to be optimal. For now, this is considered to be an open question.

Figure 1 shows the weights by year for various discount rates. A 0.1% discount rate implies that impacts 1,000 years in the future are still important. A 10% discount rate would focus primarily on the next 10–20 years. For many of our biggest policy concerns today, such as climate change, a 100 year horizon may be necessary, which would imply a roughly 1% discount rate on future happiness.

6.1 Population Constraints

Using Net Present Happiness as a metric for optimization rather than total happiness as in Eq. 1 solves the problem of future generations, but some aspects of population are

¹ Without assuming any form of faster-than-light travel, some speculate that humanity could colonize the galaxy within one million years. Humans only invented agriculture 12,000 years ago. If we consider the full potential future of humanity, the only decisions having any value would be those that promote galactic colonization. Earth might be nothing more than an expendable resource when seeking to colonize a galaxy. Such hypotheticals can make for entertaining science fiction, but are useless in designing an AI objective function of practical value.

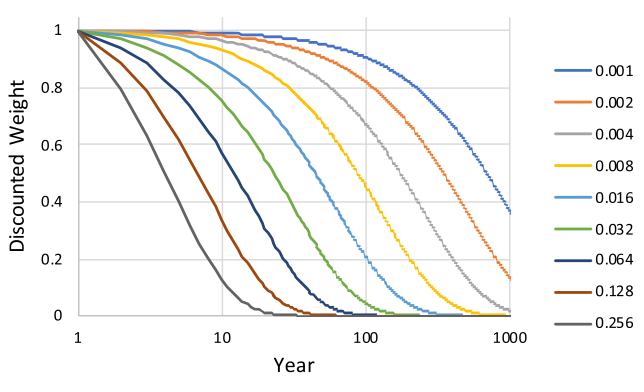
Fig. 1 Annual weights from various discount rates

still unresolved. Science fiction stories are replete with utopian communities of ten thousand or a hundred thousand people living within a futuristic theme park. Technology does not work that way. If the human society of today suddenly shrank to one million people, our factories would go dark and the knowledge that operated them would disappear. To sustain our standard of living and subjective well-being, we need a minimum number of people to sustain our technology.

The population sufficient to maintain a specific level of technology must depend upon that technology. Looking through human history, we have observations of what level of technology was possessed by societies of a certain size. When humans introduced trade, technological maintenance became dependent upon the full network of those societies. To maintain the technology of today, we likely require some number of people close to what we have today.

So far this discussion assumes that humans are required to store and utilize the technology of a society. Could we be on the verge of changing that? Wikipedia, large language models (LLM) [53], robotic factories and farm workers, and future advances in AI may allow for a smaller population of humans that no longer operate all of the machines to sustain our standard of living. Advances in 3-D printing and micro-manufacturing might eliminate the need for some massive, labor-intensive factories, allowing for even fewer humans.

The $N(s, t)$ in Eq. 9 reflects how many people are predicted to exist in a community, but the equation overall could also incorporate a penalty for falling below the number of people predicted to be required to maintain our technology. Over the next 10 years, that minimum number could be taken as the same number required today. On longer horizons, there could be less penalty to NPH as policy suggestions create fewer, happier people and the technology is maintained by other means.

The penalty function for having too few humans to maintain our standard of living must be highly nonlinear. Our technology is very interconnected, so breaching the

minimum number could lead to cascade failures. If $sigma$ is the standard deviation of log(SWB) and FB is similarly scaled after adjustment for fairness, then the penalty for breaching technological sustainability could be expressed in standard deviations $sigma$:

$(12) quad Phi(N(t)) = text{FB} - begin{cases} alphasigma log left( frac{N(t)}{N_B(t)} right) & N(t) < N_B(t) 0 & N(t) ge N_B(t) end{cases}$

In Eq. 12, $N_B$ is the baseline level of population required to maintain our standard of living and $alpha$ is a scaling factor. The definition of SWB is on a 20-point scale, and log(SWB) is approximately normally distributed with a standard deviation of $sigma = 3.84$. Setting $alpha = 9.5$ would create a penalty of $-1sigma$ if N is 90% of $N_B$ and $-2.1sigma$ if N is 80% of $N_B$. $alpha$ would be tuned during testing of an AI recommendation ranking score to minimize the risk of unsustainable population reduction.

The global shortages caused by supply chain constraints from the COVID-19 pandemic and war in Ukraine [54, 55] serve as proof of how interdependent our world has become. As soon as we assume that one country or region is relatively unimportant to global conditions, we can trace the supply chain dependencies to identify unique resources or services provided by the location.

As a simple start to understanding the baseline population required today, $N_B(t = 0)$, this baseline must include employed people, caregivers raising the next generation who may not be counted as employed, students, and children. The only groups that may not be included in $N_B$ would be retirees and future excess births, on the assumption that they are not necessary to maintaining our technology or creating future generations. This in no way should encourage the AI to disregard retirees. It simply means that the population for a given country today is always greater than the technologically necessary minimum. The penalty in Eq. 12 applies only if the total population falls below this threshold.

The baseline population could change due to technology advances or be a specific goal of the AI’s recommendation. However, the baseline population at any time $t$ must incorporate disruptions from rapid population change. Predicting $N_B(t)$ to avoid disruption from rapid change could be part of the AI’s recommendation or from a separate algorithm tasked with generating a population ethics score for the AI’s recommendations.

Equation 12 does not consider upper bounds on population that make sustaining our current standard of living impossible. That is even harder to judge given the range of climate change scenarios from human activity and the many counter-balancing and adaptive technologies that could allow humanity to continue. The present formulation assumes that those effects will appear directly in the model of SWB as we, or the AI, learn more about how climate change will impact humanity’s subjective well-being.

7 Risk of Failure

In assembling an objective function for scoring AI policy recommendations, the final component is to consider the risk of failure. When comparing two possible recommendations of equal predicted benefit, the preferred choice is obviously the less risky one. In this case, the uncertainty in the predicted change in Net Present Happiness, $Deltatext{NPH}$ must be considered. Regression equations that produce a model, M, naturally provide confidence intervals on their forecasts, but this does not reflect all of the uncertainty.

A hypothetical AI policy recommendation invariably impacts the many interconnected systems of our society, now and in the future. Part of that AI or an assessment wrapper attached to it must predict how all of the inputs to the model for FB, such as in Eq. 3, will change. Such predictions will invariably involve uncertainties and distributions of possible impacts. As each simulation incorporating one sample from these distributions of uncertainties is fed through Eq. 10 to predict $Deltatext{NPH}$, a distribution of the possible outcomes can be created. The simulations and the final distribution should also consider uncontrollable events such natural disasters, human-caused unexpected events, etc. This process is exactly how financial institutions must prepare for unexpected events when they compute capital reserves. For a specific financial investment, the expected return divided by the uncertainty in the return is called the Sharpe Ratio [56]. To create a complete score of an AI recommendation, we need a comparable ratio comparing the expected gain in subjective well-being to the uncertainty in achieving that result, Eq. 13:

$(13) quad S = frac{Deltatext{NPH}}{sqrt{text{Var}(Deltatext{NPH})}}.$

The financial risk management literature goes into great detail on how best to compute risk-adjusted returns. The Sharpe ratio penalizes equally for unexpected gains and unexpected losses, although only unexpected losses are undesirable. A better approach is the Sortino Ratio [57], Eq. 15 which only penalizes for negative outcomes:

$(14) quad text{Sortino} = frac{Deltatext{NPH}}{sqrt{text{DownsideVar}(Deltatext{NPH})}}$

$(15) quad text{DownsideVar} = frac{1}{n}sum_{i=1}^{n} (min(0, Deltatext{NPH}))^2.$

Both of these expressions look at one standard deviation events. If the distribution of $Deltatext{NPH}$ outcomes is tabulated via simulation by the AI, then a more stringent criteria can be set. Financial institutions usually prepare for 1-in-1000 year events by setting aside additional capital. When scoring recommendations, the risk adjustment could similarly adjust for "tail risk". Even the best recommendation may have sufficient risk that the AI should then be asked for the best risk-mitigating action.

Equation 15 leads to an AI objective function for Risk-Adjusted Gain in Net Present Happiness.

8 Conclusions

The discussion of AI ethics changes when considering whole societies or all of humanity. Considerations of fairness require minimizing harm, distributing it appropriately, and ensuring that it is an investment into creating greater well-being for everyone in the future. To solve the problem of ranking AI policy recommendations, we need to bring together insights from philosophy (population ethics), psychology (happiness studies), finance (net present value and risk management), and economics, among other fields. This research has found that these ideas are not only complementary, but actually solve some problems that have arisen when they are studied in isolation, like the Repugnant Conclusion in population ethics.

Humans naturally balance multiple benefits and penalties when choosing among alternatives. Although we cannot consciously express this process as a single function, our judgments imply an assessment weighted by the relative importance, certainty, and temporal proximity of the components. For our AI, we will need to create such an objective function or in cases where the expression is too complex and nonlinear, to train the AI to have an internal representation of the goal that must be optimized. Inevitably, the objective function must be a weighted combination of the benefits and costs, financial, environmental, ethical, etc. This necessitates a combination of economic and ethical considerations when making any decision, just as humans use.

Many researchers have recognized the risks of giving an AI an overly specific and limited goal. Humanity is complex and what we ask, even if provided exactly as specified, may not be what we need or actually want. Indirect normativity refers to asking the AI to "Do whatever we would have the most reason to ask the AI to do." [58] Ultimately, an approach like this may be exactly what we need, but to decipher such a directive requires a deep understanding of humanity. No AI, no matter how intelligent, can determine what will make humanity happy without data. A computer simulation of humanity cannot be used to generate the needed data the way AlphaGo did to solve the game of Go, because we are still learning the rules of humanity’s happiness.

Similarly, if the only goal of the AI system during training is to optimize its own assessment of humanity’s future happiness, a result similar to the wire-heading problem [58, 59] may allow the AI to delude itself into thinking that all of its recommendations are wonderful simply because its forecast accuracy is terrible. The primary goal of the AI system during training must be forecast accuracy. The assessment of benefit in the form of Risk-Adjusted Gain in Net Present Happiness or any other metric is an additional algorithm. This too is very similar to the dual-algorithm approach of AlphaGo [60].

For the intellectually limited AI systems being created today, researchers need to provide a digested, more actionable Beta Version of the indirect normativity goals rather than leave these systems with narrow, amoral objective functions. AI researchers are already attempting to create AI systems that can make policy recommendations, so we should consider the value of including a reasonable first approximation of collective benefit as part of an AI’s objective function. Risk-Adjusted Gain in Net Present Happiness appears to possess the key ingredients to be a beta solution for an AI in training. However, we will always run the risk that optimizing collective well-being did not lead to the best outcome for humanity. The adjustment for fairness is one such example. AI researchers will need to carefully track the research of psychologists, sociologists, and ethicists in order to adapt to new insights. We cannot assume that an AI system will figure out what is best for humanity if we cannot gather the necessary data and relationships.

Declarations

Conflict of interest: On behalf of all the authors, the corresponding author states that there is no conflict of interest.

Open Access: This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

References

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.