Solving the Long-Range Forecasting Problem in Supervised Learning

Abstract 

In a world where big data is everywhere, no one has big data relative to the economic cycle. Data  volume needs to be thought of along two dimensions. (1) How many accounts / transactions / data  fields do we have? (2) How much time history do we have? Few, if any, big data sets include history  covering one economic cycle (back to 2005) or two economic cycles (back to 1998). Therefore,  unstructured learning algorithms will be unable to distinguish between long-term macroeconomic  drivers and point-in-time variations across accounts or transactions. This is the colinearity problem that  is well known in consumer lending. 

This paper presents a solution to the colinearity problem in the context of applying neural networks to  modeling consumer behavior. An initial model is built using methods that are specifically tuned to  capture long-term drivers of performance. That model is treated as given information to a neural  network that then learns potentially highly non-linear dynamics relative to the given knowledge. 

This approach of incorporating given knowledge into a supervised learning algorithm solves a deep but  rarely recognized problem. In short, almost all models created via supervised learning will not give  correct long-range forecasts when long-term drivers are present without corresponding data covering  multiple cycles for those drivers. Thus, the need for such a solution is great and the solution provided  here is sufficiently general that it can apply to a broad range of applications where both high frequency  and low frequency drivers are present in the data.

1. Introduction 

Creating forecasting models for target variables that are impacted by both internal and external drivers is a well known problem for statistical modeling. Examples of this include modeling consumer spending  that is impacted by consumer behavior (internal) and economic factors (external) or credit risk modeling  where delinquency (internal) and economic factors (external).  

Since the internal and external factors can be correlated, properly separating effects is essential for  accurate forecasting. Solving the problem is complicated when the external drivers have a short amount  of data, such as economic factors. Learning algorithms have been very successful modeling large  datasets when any cycles present are observed multiple times. However, in the case of economic data,  the history is very short relative to the economic cycle, so mixing a short history for economics with a  large data set for internally observed performance factors is a classic example of this problem.  

This situation has previously been solved for regression-type models (Breeden, 2016). In the specific  context of creating loan-level stress test models of consumer loan delinquency, an Age-Period-Cohort  model was used to capture two specific external drivers, economic impacts on delinquency versus  calendar date and lifecycle impacts versus the age of the loan. This first stage modeling captures the  long-term variation in consumer loan delinquency. The economic and lifecycle effects were then fed into  a regression model as a fixed offset, meaning that their coefficients are each 1.0 in the final model. All  other coefficients in the regression equation that are estimated on consumer behavioral attributes are  estimated such that they provide adjustments relative to the fixed offsets but without changing those  offsets. In this way, no problem arises from multicolinearity, because the offsets are taken as primary  and the other coefficients capture the residuals. 

In supervised learning generally, the training data contains observed values of a target variable and a set  of candidate explanatory variables (Reed and Marks, 1999). Supervised learning has been used  previously for predicting time series such as economic time series (Chakraborty, et. al., 1992; Kaastra, et.  al, 1996) and separately for intrinsic behavior patterns such as credit scoring for offering consumer loans  (West, 2000; Angelini, et. al., 2008). The problem just described in the context of regression models also  applies more generally across supervised learning algorithms, where the same multicolinearity problem  persists. However, many of those algorithms are unstructured and therefore lack the tools needed to  solve the multicolinearity problem in a robust manner. 

2. Modeling Approach 

The present solution to the multicolinearity problem is a two-stage modeling approach. A first model is  created that estimates future changes in long-term performance drivers. This could be an econometric  model, survival model, or other types that capture long-term changes relative to calendar date or age of  an account. This could more generally be treated as “given knowledge” obtained from models on other data sets or other sources. This given knowledge is treated as a fixed, known input to a second model, a  supervised learning approach that may have much richer information to train on over a shorter time  frame that what originally created the given knowledge. 

If the target variable for the analysis is real valued, then the solution is simple. The forecasts from the  given knowledge are subtracted from the target variable to obtain residuals. The supervised learning  algorithm is applied to predicting the residuals. However, binary target variables are much more  challenging. 

Many popular data mining techniques for binary data are discrimination models that attempt to group  1s and 0s according to boundaries defined along explanatory variables. Decision trees, random forests,  and support vector machines are all examples of this. Incorporating given knowledge into a  discrimination method is difficult, because the equivalent to modeling residuals for continuous  variables, such as trying to adjust the 0s and 1s, is not well defined. Instead, a more natural approach is  to use a probabilistic method like neural networks where the given information can be incorporated into  the architecture of the network and the output can be a continuous variable between 0 and 1. 

Using neural networks as an example probabilistic method and predicting mortgage defaults as a target  case, we can develop a specific model that incorporates given information into a flexible nonlinear  structure. 

    2.1.Model of Given Knowledge 

In modeling loan defaults, the given knowledge required here corresponds to long term variation due to  lifecycle effects versus the age of the loan and macroeconomic effects versus calendar date. When  modeling mortgage defaults, a cycle in either of these drivers can be five to ten years. Age-Period-Chort  models (Holdford 1983) provide one robust method to modeling these. An Age-Period-Cohort model of  a binary outline is structured as 

Def(I,a,v,t) ~ F(a) + G(v) + H(t)     Eq.1 

Where F(a) is the lifecycle with age of the loan, G(v) is the credit quality by origination cohort (vintage),  and H(t) is the environment function (macroeconomic effects) by calendar date. F, G, and H are  frequently estimated via splines or nonparametrically as 

F(a) = sum_a (alpha_a delta(a)) 

G(v) = sum_v (beta_v delta(v)) 

H(t) = sum_t (gamma_t delta(t)) 

Where delta(i) = { 1 if i = a, 0 if i <> a}

In the current work, and Bayesian APC algorithm (Schmid and Held, 2007) is used to solve the logistic  regression maximum likelihood function corresponding to Eq. 1.  

To create this solution, a constraint must be applied, because a linear relationship between age, vintage,  and time exists, a = t – v. That linear relationship is one of the sources of the colinearity problem. In an  APC model, it appears as a linear specification error in age-vintage-time. Any solution to the  specification error is domain specific. Breeden and Thomas propose one such solution (Breeden and  Thomas, 2016). 

Many organizations are able to provide the necessary data to estimate the APC model in Eq. 1. That data  often extends to ten or twenty years, which is sufficient to measure these functions and apply an  appropriate constraint to solve the specification error. By contrast, detailed behavioral loan-level  information is often available only for a few years. Very few organizations can provide such information  as loan delinquency going back before the 2009 recession. Almost none have such data back to the 2001  recession. Therefore, when estimating the full loan-level model, the functions and constraints created  here must be preserved structurally. 

    2.2.Model of Learning Algorithm with Given Knowledge 

Incorporating given knowledge as a fixed input into a learning algorithm is equivalent to having that  information persist through to the final output with coefficient 1.0. Such an architecture for a neural  network is shown in Fig. 1.

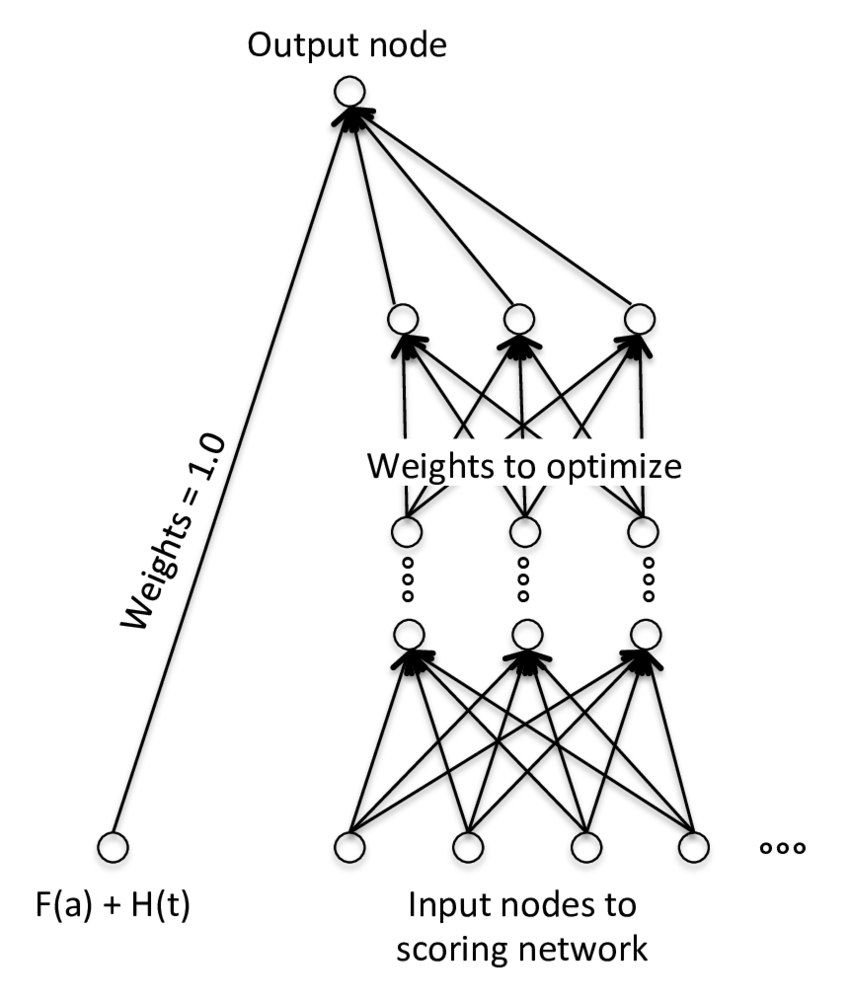
Figure 1: Network architecture for a neural network with given knowledge. 

The neural network is effectively in two parts. One part passes the given knowledge unchanged to the  end node. The other part is unconstrained as it may take on any structure needed to capture the full  nonlinearity of the available data. The only additional constraint is that the output node must be  consistent with the training of the given knowledge. In the case of our APC model, that was a logistic  regression where the original G(v) function is being replaced with the learning part of the neural  network. In the language of the neural network literature, that corresponds to a cross-entropy optimization. 

3. Numerical Example 

To demonstrate modeling the APC + neural network model, we used publicly available data from Fannie  Mae and Freddie Mac on mortgage loan performance to predict mortgage defaults. The data was loan level spanning a period from 2005 to 2017. The APC model was trained first on a vintage-level aggregation of the data using a Bayesian APC algorithm.  The functions estimated were published  previously (Breeden 2018). 

Analogously to the multihorizon discrete time survival model developed previously (Breeden, 2018), the  lifecycle and environment functions were taken as inputs to the creation of a neural network as shown  in Fig. 1. The input nodes included behavioral factors of credit score, LTV, loan purpose, etc. The inputs  were measured monthly for each account. The output node would be used to predict the log-odds of  default each month for each account. It is important not to threshold the final output node to a binary  forecast. For mortgage defaults, almost all probabilities for default are less than 0.5, so thresholding  would bias the forecast toward non-default. 

In the tests on the mortgage data, this approach was effective at combining the given knowledge from  the APC algorithm with the neural network. This was a test of effectiveness of the approach, not a  specific attempt to out-perform the existing discrete time survival model. That said, the APC + NN model  performed almost as well as the best case discrete time survival model. 

4. Conclusions 

The modeling approach described in this paper solves a problem most likely present in every application  of supervised learning to consumer behavior and other applications where long-term drivers are present  on scales greater than the available data sample. The multicolinearity problem relative to long time  scale drivers will not be apparent when only short range forecasts are made, but product pricing,  financial planning, and regulatory compliance all rely on long-range predictions. 

The final solution of using a two-stage modeling approach and a specific architecture as shown in Fig. 1  seems simple on the surface, but represents a dramatic change to how data mining is currently being  applied in these areas. Getting the details correct for the architecture and activation functions creates  the stability needed for long-range forecasting. 

Further, the approach here of incorporating given knowledge can be used much more widely. The given  knowledge could more generally be based upon business intuition or other non-model inputs. We  intend to explore that further as it can expand the use of supervised learning into augmenting decision making where full automation is not feasible.  

Acknowledgements 

This work was supported by Prescient Models LLC and is patent pending.